1.
Reviews
1 / 7

2 / 7

3 / 7

4 / 7

5 / 7

6 / 7

7 / 7

IGCSE Mathematics Worksheet - Venn Diagrams 2
Answer the following
1. Kim collected data on 40 people’s enjoyment of sport.P is the set of people who play sports regularly, and
W is the set of people who watch sports regularly.
3. Jack asked 60 people which sports they liked from rugby, football and cricket.
8 people like all three sports.
17 people like rugby and football.
13 people like football and cricket.
19 people like rugby and cricket.
35 people like football.
27 people like cricket
30 people like rugby.
4. Jenny asked 80 people which sports they enjoy from Football, Hockey and Rugby.
Find the probability of:
(a) How many people enjoy all three sports?
(b) How many people enjoy football and hockey but not rugby?
(c) How many people enjoy football and rugby but not hockey?
(d) Work out which sport is enjoyed by the most number of people.
R = red cars
J = cars manufactured in Japan
32 of the people she asked watch sports regularly.
An incomplete Venn diagram for her data is shown below.
a) Complete the Venn diagram.
b) Work out P(W∪P) for someone picked at random.
c) Work out the probability that someone picked at random watches sports regularly but not play sports regularly

All 50 people like at least one of the drinks
19 people like all three drinks.
16 people like tea and coffee but do not like milk.
21 people like coffee and milk.
24 people like tea and milk.
40 people like coffee.
1 person likes only milk.
Sami selects at random one of the 50 people.
Draw a Venn Diagram and Work out the probability that this person likes tea.
a) Complete the Venn diagram.
b) Work out P(W∪P) for someone picked at random.
c) Work out the probability that someone picked at random watches sports regularly but not play sports regularly
2. Sam asked 50 people which drinks they liked from tea, coffee and milk.
All 50 people like at least one of the drinks
19 people like all three drinks.
16 people like tea and coffee but do not like milk.
21 people like coffee and milk.
24 people like tea and milk.
40 people like coffee.
1 person likes only milk.
Sami selects at random one of the 50 people.
Draw a Venn Diagram and Work out the probability that this person likes tea.
3. Jack asked 60 people which sports they liked from rugby, football and cricket.
8 people like all three sports.
17 people like rugby and football.
13 people like football and cricket.
19 people like rugby and cricket.
35 people like football.
27 people like cricket
30 people like rugby.
Draw a Venn Diagram and Work out the probability that people liked neither rugby or football or cricket?
4. Jenny asked 80 people which sports they enjoy from Football, Hockey and Rugby.
Find the probability of:
(a) How many people enjoy all three sports?
(b) How many people enjoy football and hockey but not rugby?
(c) How many people enjoy football and rugby but not hockey?
(d) Work out which sport is enjoyed by the most number of people.
5. The Venn diagram shows information about the cars in a car park.
ξ = 150 cars in the car parkR = red cars
J = cars manufactured in Japan
A car is chosen at random.
Work out the probability that it is red.
Work out the probability that it is red.
GCSE, IGCSE Mathematics Worksheet - Number
Answer the following
1. A rare stamp is worth €2500 and depreciates by 8% p.a. Find the value of the stamp after one year.
2. A rare sculpture is worth €120 000 and appreciates by 8% p.a. Find the value of the sculpture after one year.
3. Find 15 km as a percentage of 120 km
4. Find 70% of 24 hrs.
5. Olive measures Salma’s height as 95 cm. Some time later she measures her height as 1.14m.
6. Work out the percentage increase in Salma’s height.
7. Indira’s swimming time decreases from 32 s to 24 s. Work out the percentage decrease in her time.
8. Erika’s toy ski chalet is valued at €450. Its value increases by 10% then decreases by 10%
the year after. What is the value of Erika’s toy after these two changes?
9. Luke’s salary changes from €75 000 p.a. to €100 000 p.a. Find the percentage increase in Luke’s salary.
10. Mari’s watch gains 3 minutes every hour. Find the percentage error in Mari’s watch at the end of one hour.
11. Increase $350 by 17.5%.
12. Decrease $350 by 17.5%.
3. Find 15 km as a percentage of 120 km
4. Find 70% of 24 hrs.
5. Olive measures Salma’s height as 95 cm. Some time later she measures her height as 1.14m.
6. Work out the percentage increase in Salma’s height.
7. Indira’s swimming time decreases from 32 s to 24 s. Work out the percentage decrease in her time.
8. Erika’s toy ski chalet is valued at €450. Its value increases by 10% then decreases by 10%
the year after. What is the value of Erika’s toy after these two changes?
9. Luke’s salary changes from €75 000 p.a. to €100 000 p.a. Find the percentage increase in Luke’s salary.
10. Mari’s watch gains 3 minutes every hour. Find the percentage error in Mari’s watch at the end of one hour.
11. Increase $350 by 17.5%.
12. Decrease $350 by 17.5%.
GCSE Mathematics Worksheet - Probability
Answer the following
3. There are 300 seeds in a packet of flower seeds.Each seed will grow into a white flower or a yellow flower or a red flower. The probability of a seed growing into a white flower is 0.62. 45 of the seeds are expected to grow into yellow flowers. One of the seeds is chosen at random from the packet. What is the probability that this seed will grow into a red flower?
1. What is the probability of picking two doubles from a pack of dominoes? [Hint: There are 50 dominoes in a pack. 7 of them are doubles.]
2. John picks a card at random from a pack of 52 cards and throws a dice. What is the probability that he will pick the ace of spades and throw a six?
2. John picks a card at random from a pack of 52 cards and throws a dice. What is the probability that he will pick the ace of spades and throw a six?
3. There are 300 seeds in a packet of flower seeds.Each seed will grow into a white flower or a yellow flower or a red flower. The probability of a seed growing into a white flower is 0.62. 45 of the seeds are expected to grow into yellow flowers. One of the seeds is chosen at random from the packet. What is the probability that this seed will grow into a red flower?
4. Martin has a pencil case which contains 4 blue pens and 3 green pens. Martin picks a pen at random from the pencil case. He notes its colour, and then replaces it. He does this two more times. Work out the probability that when Martin takes three pens, exactly two are the same colour.
5. Natalie has 8 socks in a drawer.
5 of the socks are black.
3 of the socks are white.
Natalie takes out a sock at random, writes down its colour and puts it back into
the drawer.Then Natalie takes out a second sock, at random, and writes down its colour. Draw tree diagram and Work out the probability that the two socks are the same colour.
5 of the socks are black.
3 of the socks are white.
Natalie takes out a sock at random, writes down its colour and puts it back into
the drawer.Then Natalie takes out a second sock, at random, and writes down its colour. Draw tree diagram and Work out the probability that the two socks are the same colour.
Download from www.qusaistuition.com
IGCSE Mathematics Worksheet - Differentiation (Calculus) -1
Answer the following
1.


Find the maximum value of A.
2.


(c) State whether the turning point is a maximum or a minimum.
3.

4.

Find the coordinates of the point of y=f(x) where the gradient is 8
5.

Downloaded from https://qusaistuition.blogspot.com
(c) State whether the turning point is a maximum or a minimum.
3.
4.
Find the coordinates of the point of y=f(x) where the gradient is 8
5.
Downloaded from https://qusaistuition.blogspot.com
IGCSE Mathematics Worksheet - Vectors-2
Answer the following
1.
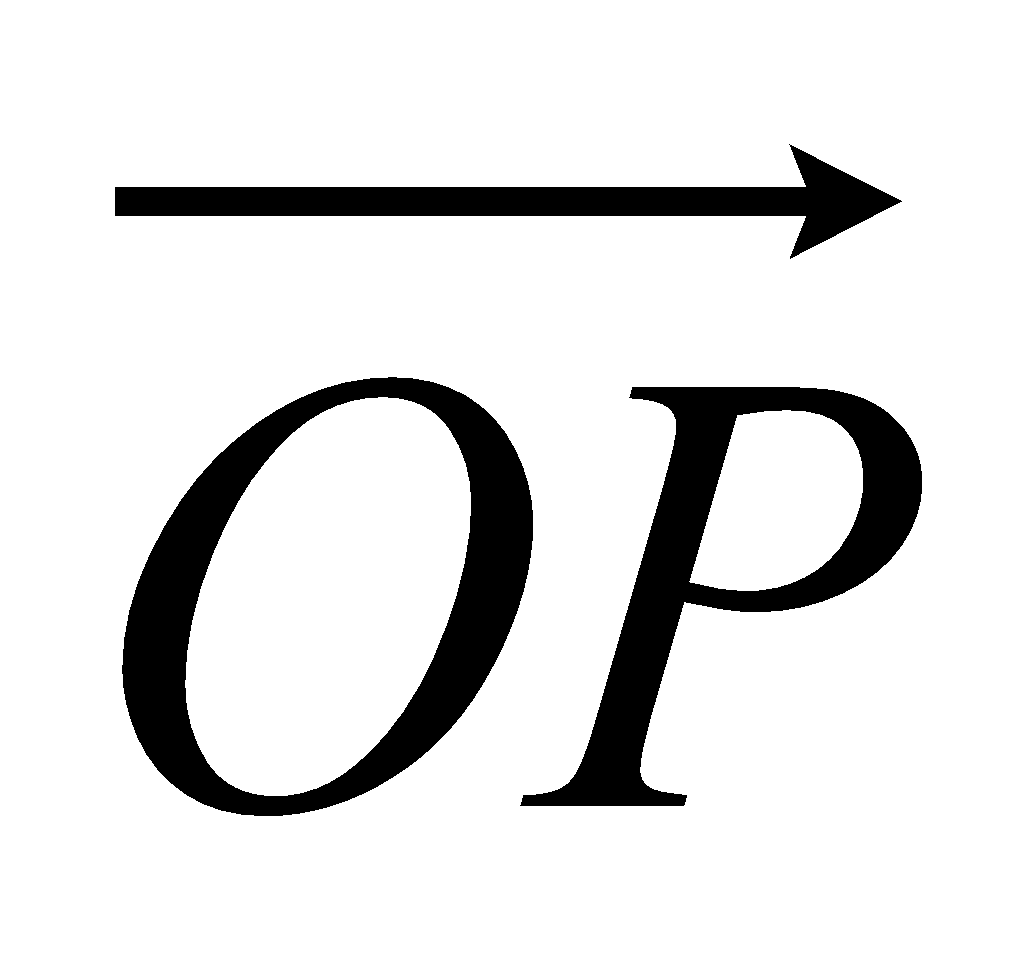
OPQ is a triangle. T is the point on PQ for which PT : TQ = 2 : 1.
 = a and
= a and  = b.
= b.
(a) Write down, in terms of a and b, an expression for  .
.
(b) Express 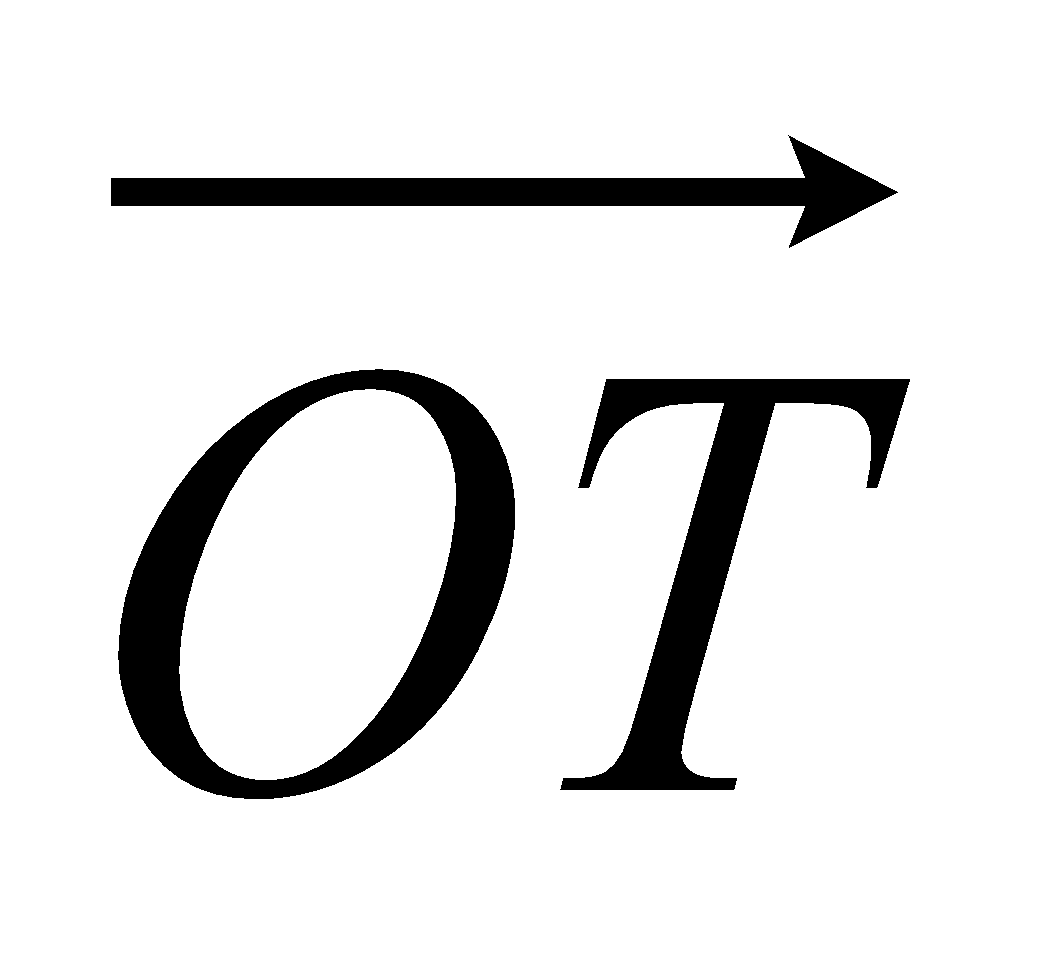 in terms of a and b. Give your answer in its simplest form.
in terms of a and b. Give your answer in its simplest form.
2.
ABCD is a parallelogram. AB is parallel to DC. AD is parallel to BC.  = p
= p  = q
= q
Express, in terms of p and q
(i) 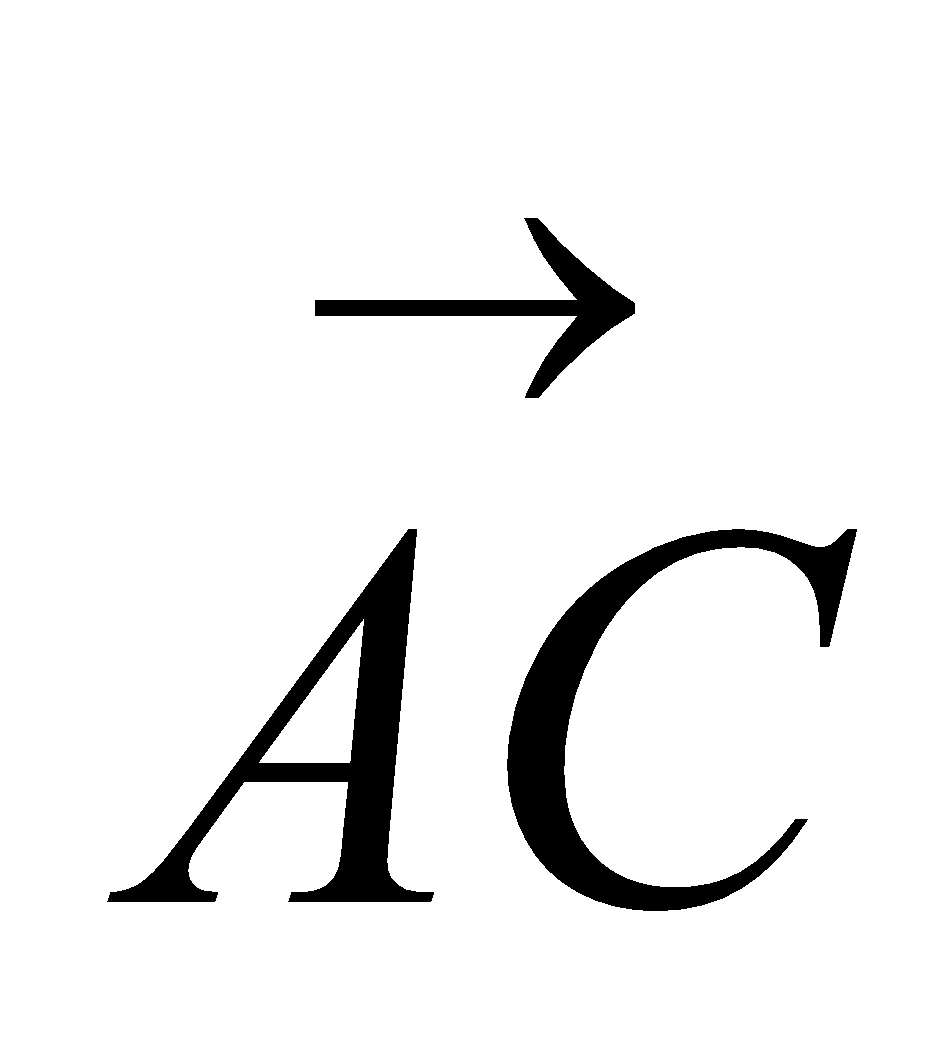
(ii) 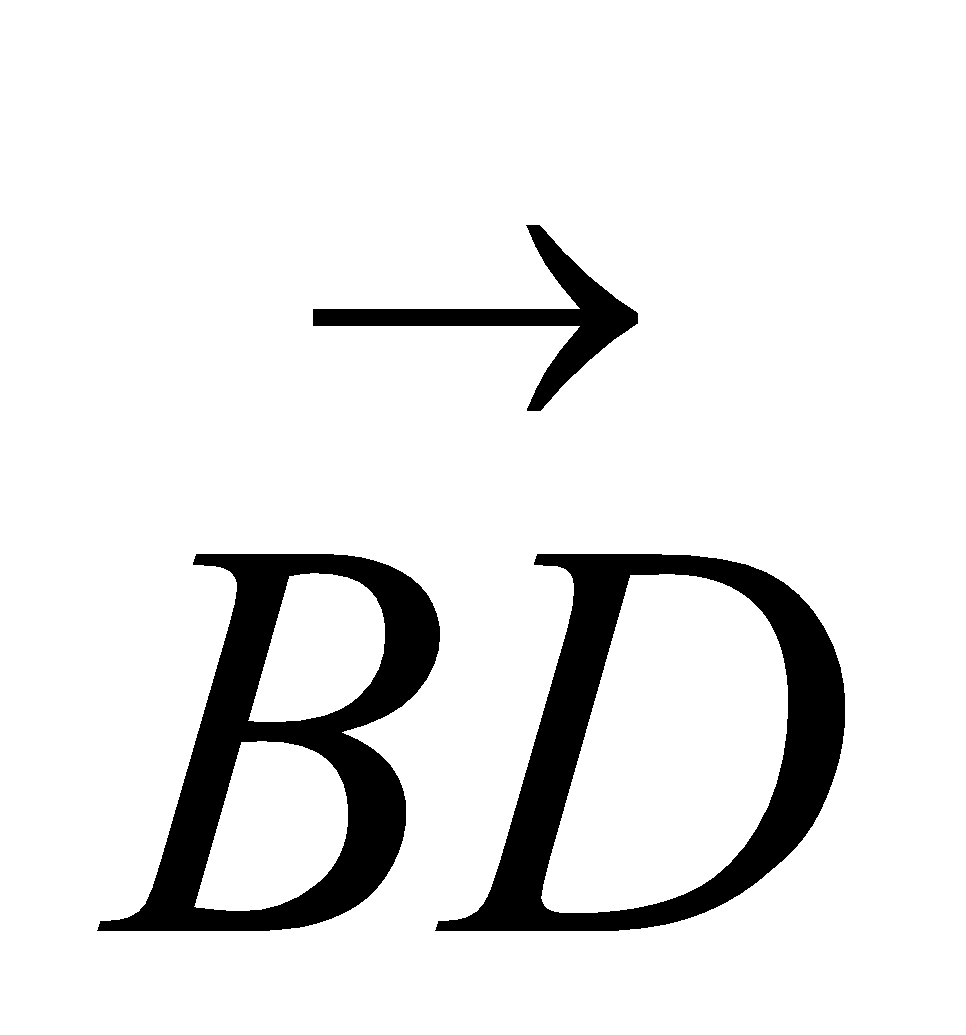
3.
M is the midpoint of PQ and N is the midpoint of OR.
(a) Find the vector 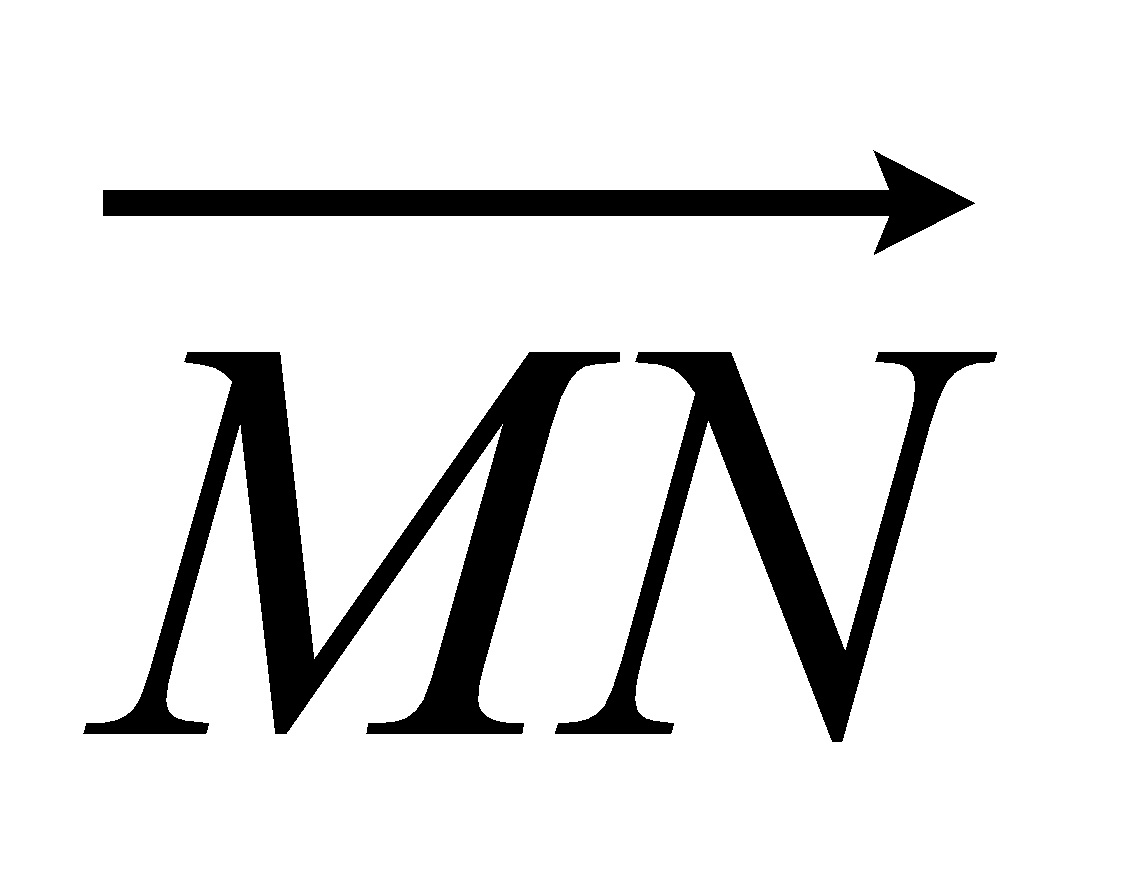 in terms of a and b.
in terms of a and b.
X is the midpoint of MN and Y is the midpoint of QR.
(b) Prove that XY is parallel to OR.
4. (a)Express in terms of a and/orb
(i) 
(ii)

X is the midpoint of BC.
(b) Express 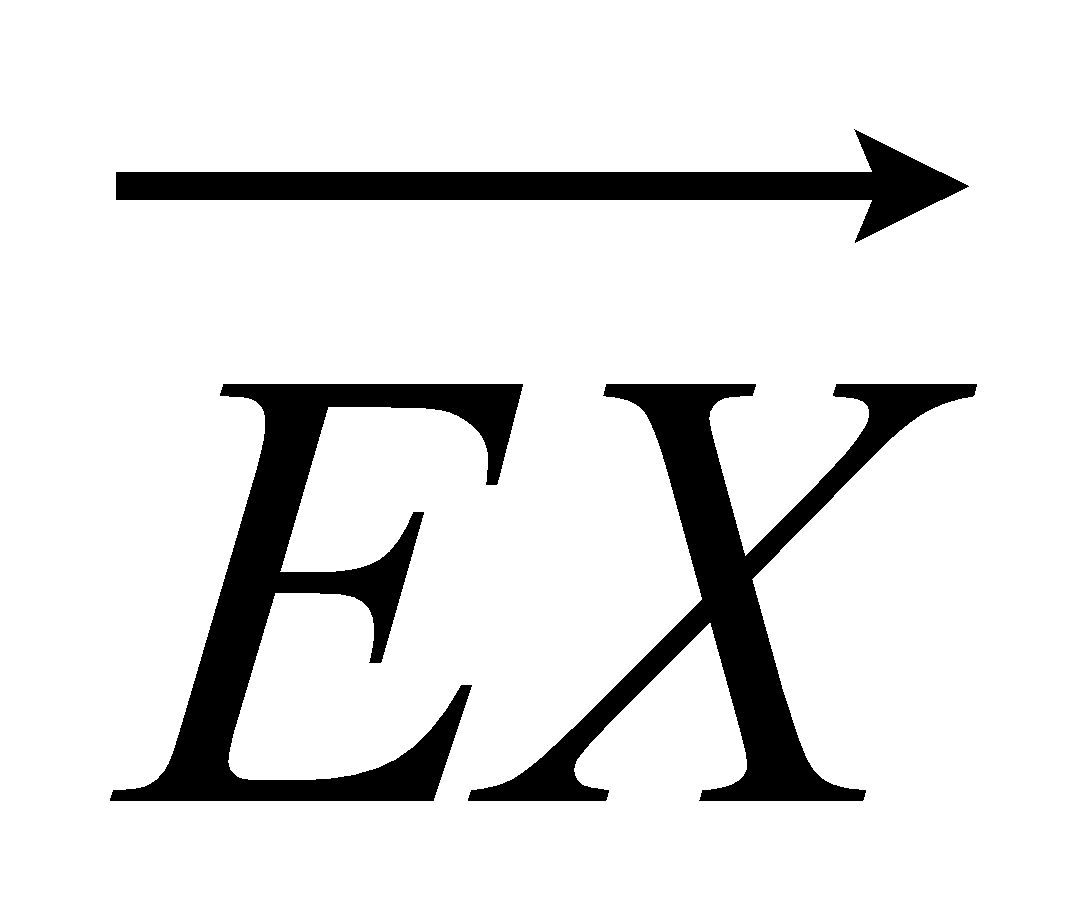 in terms of a and/or b
in terms of a and/or b
Downloaded from https://qusaistuition.blogspot.com
IGCSE CIE Mathematics Revision Sheet - 1
Marks: 48
Answer the following
1.

(a) (i) Draw the reflection of triangle T in the line x = 0. [2]
(ii) Draw the rotation of triangle T about (–2, –1) through 90° clockwise. [2]
(b) Describe fully the single transformation that maps triangle T onto triangle U. [2]
2.
(a) (i) Draw the reflection of triangle T in the line x = 0. [2]
(ii) Draw the rotation of triangle T about (–2, –1) through 90° clockwise. [2]
(b) Describe fully the single transformation that maps triangle T onto triangle U. [2]
2.
b)
3.
(b) Find f -1(x). [2]
(c) Find gf(x) in its simplest form. [3]
(d) Solve the equation h-1(x) = 0.5 [1]
AB is parallel to DC.
AB = 55 m, BD = 70 m, angle ABD = 40° and angle BCD = 32°.
(a) Calculate AD [4]
(b) Calculate BC. [4]
(c) Calculate the area of ABCD. [3]
5. (i) Show that the volume of a metal sphere of radius 15 cm is 14 140 cm3, correct to 4 s.f [2]
(ii)Calculate the volume of water needed to fill the tank [3]
(iii) The sphere is removed from the tank. Calculate the depth, d, of water in the tank. [2]
6.
(b) Determine whether each of the turning points is a maximum or a minimum.
Give reasons for your answers. [3]
Downloaded from https://qusaistuition.blogspot.com
GCSE Mathematics Worksheet - Compound Measures-1-Notes
Distance-time graphs

Acceleration

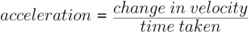

This is when:

- In a distance-time graph, the gradient of the line is equal to the speed of the object. The greater the gradient (and the steeper the line) the faster the object is moving.
- If an object is accelerating or decelerating, its speed can be calculated at any particular time by:
- drawing a tangent to the curve at that time
- measuring the gradient of the tangent
- The gradient of the line is equal to the acceleration of the object.
- The displacement of an object can be calculated from the area under a velocity-time graph.
Acceleration
- Acceleration is the rate of change of velocity. It is the amount that velocity changes per unit time.
- The change in velocity can be calculated using the equation:
- change in velocity = final velocity - initial velocity
- The average acceleration of an object can be calculated using the equation:
This is when:
- acceleration (α) is measured in metres per second squared (m/s²)
- change in velocity (∆v) is measured in metres per second (m/s)
- time taken (t) is measured in seconds (s)
- If an object is slowing down, it is decelerating (and its acceleration has a negative value).
- This equation applies to objects in uniform acceleration:
- This is when:
- final velocity (v) is measured in metres per second (m/s)
- initial velocity (u) is measured in metres per second (m/s)
- acceleration (a) is measured in metres per second squared (m/s2)
- displacement (s) is measured in metres (m)
Downloaded from https://qusaistuition.blogspot.com
Subscribe to:
Posts (Atom)









